Visual Basic - Exercice 6:

(Exercice proposé par Ruben VERA)

Projectiles

On se propose d'écrire un programme simulant la trajectoire de projectiles depuis un seul point de départ, à la manière d'un feu d'artifice. Le point initial sera choisi en cliquant sur la feuille.

Le principe :

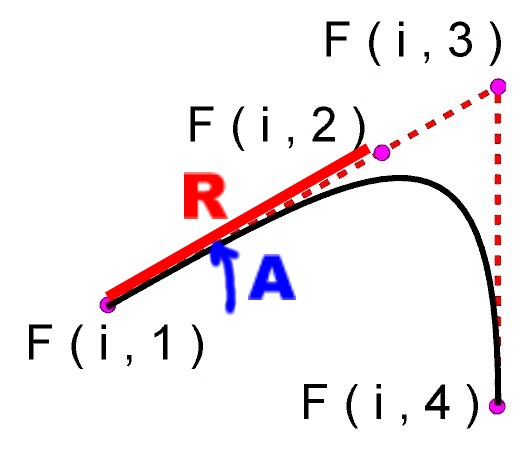
Le programme utilisera des courbes de Bézier pour représenter la trajectoire de chaque projectile. Chaque courbe nécessite quatre points de contrôle, dont deux utilisés comme extrémités. Le point cliqué F(i,1) sera le pivot depuis lequel partiront toutes les trajectoires d'une série de projectiles. Pour chaque projectile, on prendra au hasard une longueur R et un angle A en radians. R correspondra à la distance entre F(i,1) et F(i,2). F(i,3) sera dans l'alignement des deux premiers points, à une distance 3R/2 de F(i,1). Enfin, F(i,4) sera à la verticale de F(i,3) à une distance R de celui-ci (voir figure ci-contre).

Programme demandé :

Interface (voir exemple ci-dessous):

Le dessin se fera sur la feuille même, avec une échelle de 100x100 – le fond devra être en blanc

Aucun menu, aucun bouton. Seul le click de la souris sur la feuille sera intercepté. Pour des raisons pratiques, nous n'utiliserons d'ailleurs pas l'événement Click mais l'événement MouseDown.

Vous devrez écrire un module comme suit :

Soit en recopiant à la main le code inscrit au dos de cette feuille
Soit en le recopiant depuis le site http://cdalpha.univ-lyon1.fr/ruben/vb/solution3.htm

Déclarations de variables et constantes – vous devrez déclarer au moins ce qui suit :

Une constante Projectiles pour définir le nombre de projectiles par "explosion". Elle vaudra 60.
Un tableau F ( 1 to Projectiles , 1 to 4 ) de type XYPoint qui contiendra la liste des 4 points de contrôle pour chacun des projectiles
Une constante Tmax définissant le nombre maximum de valeurs de T entre F(i,1) et F(i,4), soit le nombre maximal de segments de droites pour représenter chaque courbe. Elle vaudra 100.
Un tableau FP de 4 éléments de type XYPoint qui devra recevoir les 4 points de chaque élément i de F

Une variable V de type XYPoint pour recevoir le résultat d'un calcul de courbe par V = bezier (FP, T)

Un tableau Vh pour recevoir les coordonnées du dernier point atteint pour chaque courbe à un instant T

Le code essentiel sera dans la procédure événement Form_MouseDown en deux parties distinctes :

Paramétrage des trajectoires des projectiles

Soit pour chaque projectile : une valeur aléatoire de R inférieure à 20 et un angle A quelconque.
Initialiser F(i,1) avec les valeurs X et Y qui sont fournies par Form_MouseDown
Calculer alors les valeurs X et Y pour F(i,2), F(i,3) et F(i,4)
Prévoir une valeur initiale de Vh

Lancement des projectiles

Pour chaque niveau de segment de courbe, calculer T et procéder à l'évaluation de V pour chaque projectile avant d'en tracer un segment. Vous pourrez vous inspirer de l'exemple de la "solution 3".

En cliquant au centre (avec 60 projectiles), on peut obtenir :

Code à placer dans un module :

Public Type XYPoint
X As Single
Y As Single
End Type

Public Function bezier(P() As XYPoint, T As Double) As XYPoint
     bezier.X = P(1).X * (1 - T) ^ 3 _
          + P(2).X * (1 - T) ^ 2 * 3 * T _
          + P(3).X * (1 - T) * 3 * T ^ 2 _
          + P(4).X * T ^ 3
     bezier.Y = P(1).Y * (1 - T) ^ 3 _
          + P(2).Y * (1 - T) ^ 2 * 3 * T _
          + P(3).Y * (1 - T) * 3 * T ^ 2 _
          + P(4).Y * T ^ 3
End Function

A titre d'information, voici le code de la feuille Form1 qui y était associé:

Dim P(1 To 4) As XYPoint
Dim Tmax As Integer

Private Sub Command1_Click( )
     Dim V As XYPoint
     Dim T As Double
     Dim i As Integer
     'Lecture des valeurs
     For i = 1 To 4
          P(i).X = Val(PX(i).Text)
          P(i).Y = Val(PY(i).Text)
     Next i
     Tmax = Val(T_TMax.Text)
     'Espace de travail
     Picture1.Scale (-1, 1)-(1, -1)
     Picture1.Cls
     'Calcul et dessin
     Picture1.PSet (P(1).X, P(1).Y)
     For i = 1 To Tmax
          T = i / Tmax
          V = bezier(P, T)
          Picture1.Line -(V.X, V.Y)
     Next i
End Sub

( SOLUTION DE L'EXERCICE 6 )