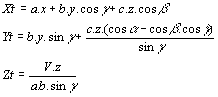Solution
![]()
Visual Basic - Exercice 1:
(Exercice proposé par Ruben VERA)
Distances inter-atomiques :
On se propose d'écrire un programme permettant le calcul de la longueur d'une liaison entre deux atomes dans un matériau, à partir des paramètres de maille (a, b, c, a , b , g ) et des coordonnées atomiques (x, y, z). Pour cela, on transforme les coordonnées (x,y,z) de chaque atome en coordonnées cartésiennes (Xt, Yt, Zt) de la façon suivante:
|
avec |
Une fois la transformation faite, l'expression pour la distance entre les atomes A1 et A2 est simplement :
![]()
Programme demandé :
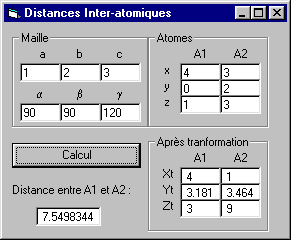
- Interface (voir exemple ci-dessous):
- Six zones de texte pour saisir les paramètres de maille (a, b, c, a , b , g )
- Six autres pour la saisie des coordonnées (x, y, z) des atomes A1 et A2
- Un bouton Calcul
- Six zones de texte pour afficher les coordonnées pour A1 et A2 après transformation – repère cartésien
- Une zone de texte pour l'affichage de la distance calculée entre A1 et A2 dans le nouveau repère
- Vous devrez écrire trois fonctions à placer de préférence dans un module (Public Function) :
- DegRad , la première, aura pour simple objectif de convertir des degrés en radians. Elle recevra donc un seul argument de type double pour retourner une valeur du même type.
- MTransform recevra les paramètres de la maille et les coordonnées d'un atome exprimées dans ce système. Le but de cette fonction est de retourner les coordonnées de cet atome transformées selon la formule expliquée plus haut.
- Distance , enfin, retournera la distance entre les deux atomes dont les coordonnées respectives lui auront été passées en arguments. Le résultat de ce calcul sera de type double.
- Le bouton Calcul ordonnera successivement les trois taches suivantes :
- Lecture des valeurs des paramètre de la maille avec conversion des angles (a , b et g ) en radians à l'aide de DegRad. Lecture des coordonnées (x, y, z) des atomes A1 et A2.
- Transformation des coordonnées de A1 et A2 dans le nouveau repère – à l'aide de MTransform. Affichage des nouvelles coordonnées.
- Calcul de la distance et affichage