Enoncé
![]()
Visual Basic - Solution 1 ( Distances inter-atomiques )
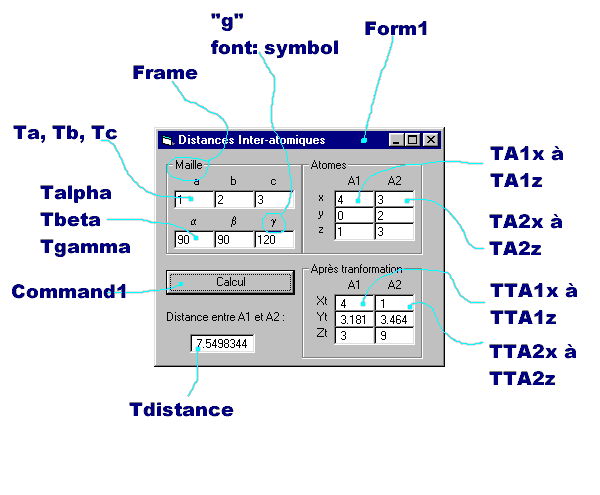
Interface graphique :
Code de la feuille Form1 :
Private Sub Command1_Click()
'Lecture des valeurs
M.a = Val(Ta.Text)
M.b = Val(Tb.Text)
M.c = Val(Tc.Text)
M.alpha = degrad(Val(Talpha.Text))
M.beta = degrad(Val(Tbeta.Text))
M.gamma = degrad(Val(Tgamma.Text))
A1.x = Val(TA1x.Text)
A1.y = Val(TA1y.Text)
A1.z = Val(TA1z.Text)
A2.x = Val(TA2x.Text)
A2.y = Val(TA2y.Text)
A2.z = Val(TA2z.Text)
'Transformation des coordonnées
At1 = MTransform(M, A1)
At2 = MTransform(M, A2)
'Affichage des coordonnées transformées
TTA1x.Text = Str(At1.x)
TTA1y.Text = Str(At1.y)
TTA1z.Text = Str(At1.z)
TTA2x.Text = Str(At2.x)
TTA2y.Text = Str(At2.y)
TTA2z.Text = Str(At2.z)
'calcul de la distance et affichage
D = Distance(At1, At2)
Tdistance = Str(D)
End Sub
Code à placer dans un module :
Public Type XYZ
x As Double
y As Double
z As Double
End Type
Public Type Maille_type
a As Double
b As Double
c As Double
alpha As Double
beta As Double
gamma As Double
End Type
Public A1 As XYZ, A2 As XYZ
Public At1 As XYZ, At2 As XYZ
Public D As Double
Public M As Maille_type
Public Const Pi = 3.14159265358979
Public Function MTransform(M As Maille_type, Atom As XYZ) As XYZ
Dim V As Double
V = M.a * M.b * M.c * _
Sqr(1 - Cos(M.alpha) ^ 2 - Cos(M.beta) ^ 2 - Cos(M.gamma) ^ 2 + 2
* Cos(M.alpha) * Cos(M.beta) * Cos(M.gamma))
MTransform.x = M.a * Atom.x + _
M.b * Cos(M.gamma) * Atom.y + _
M.c * Cos(M.beta) * Atom.z
MTransform.y = M.b * Sin(M.gamma) * Atom.y + _
M.c * (Cos(M.alpha) - Cos(M.beta) * Cos(M.gamma)) * Atom.z / Sin(M.gamma)
MTransform.z = V * Atom.z / (M.a * M.b * Sin(M.gamma))
End Function
Public Function Distance(A1 As XYZ, A2 As XYZ) As Double
Distance = Sqr((A1.x - A2.x) ^ 2 + (A1.y - A2.y) ^ 2 + (A1.z -
A2.z) ^ 2)
End Function
Public Function degrad(D As Double) As Double
'Convertion degrés >>> radians
degrad = D * Pi / 180#
End Function